devk0ng's blog HomeArchivesTagsCategories
여러 정렬에 대해 알아보자
|sorting

여러 종류의 정렬 알고리즘을 볼 때 비교 기준

  1. Stable vs Unstable : 만약 정렬하고자 하는 대상의 크기가 같은 경우, 대상들의 순서가 보장이 되는지(stable) 안되는지(unstable)
  2. In-place vs out-of-place : input에 대해 extra memory 없이 transform한다(in-place), 그렇지 않다 (out-of-place)
  3. 시간복잡도, 공간복잡도




정렬 알고리즘 종류


선택정렬(Selection Sort)


원리

: 선택정렬 알고리즘은 장소를 먼저 선택한다고 생각하면 좋을 것 같다!

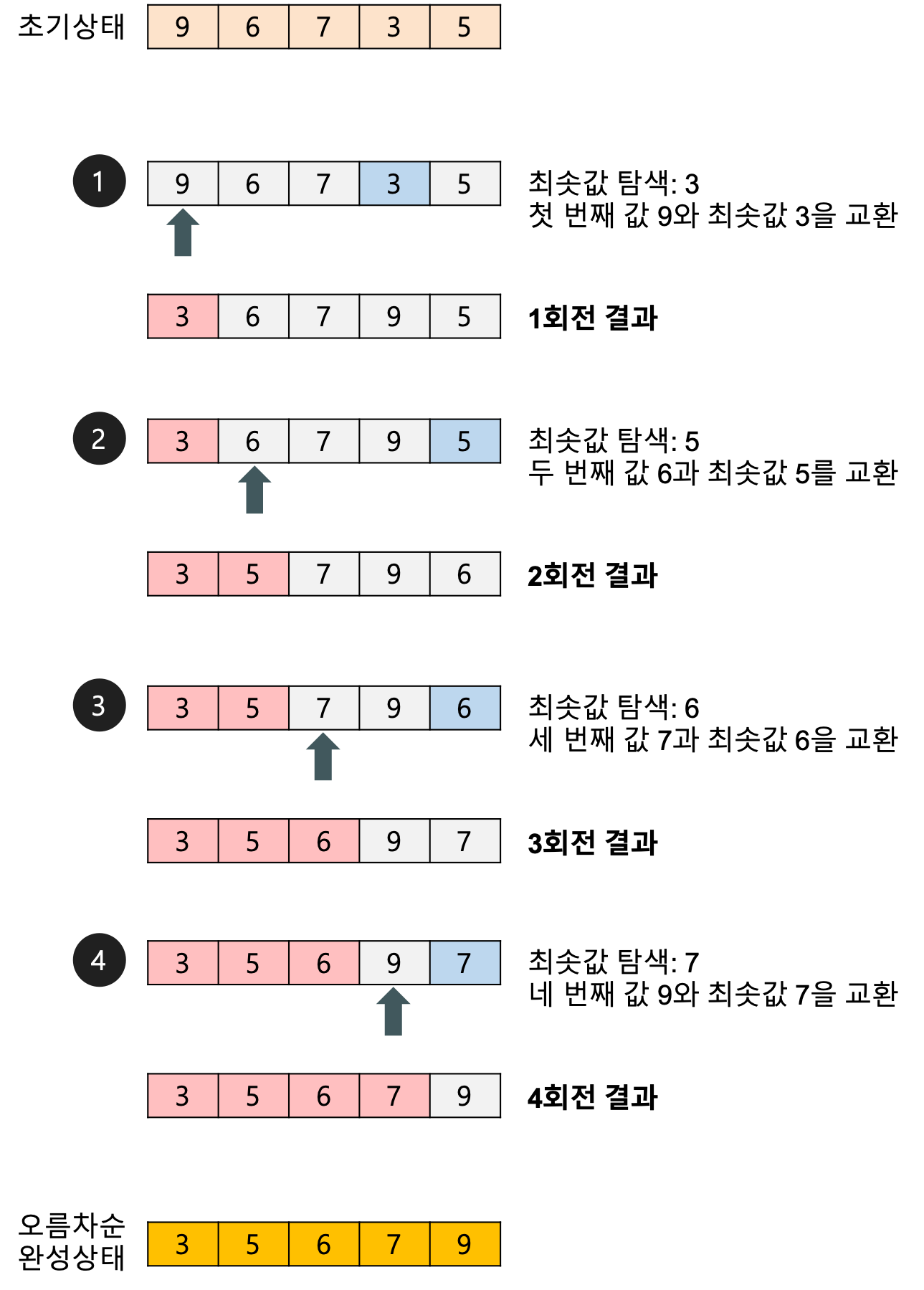
위의 그림처럼 먼저 첫번 째 자리(장소)를 선택 후 해당 자리에 어떤 숫자를 넣을지 찾는 것이다. 그리고 이 과정을 첫번째 자리, 두번째 자리.. N번째 자리까지 찾으면 정렬이 완료되는 것이다!

오름차순 정렬을 원한다면, 첫번 째 자리부터 계산을 할 때 작은 값을 선택하면 되는 것이고

내림차순 정렬을 원한다면, 큰 값을 선택해 나가면서 자리를 채워주면 되는 것이지.


코드

1
2
3
4
5
6
7
8
9
10
11
12
void selectionSort(vector<int> &arr) {
	for(int i=0 ; i<arr.size() ; i++) {
		int cur = i;

		for(int j=i+1 ; j<arr.size() ; j++) {
			if(arr[j] < arr[cur])
				cur = j;
		}

		swap(arr[i], arr[cur]);
	}
}

특성

  • 위 코드에서 볼 수 있듯이 시간복잡도는 O(N^2)이다.
  • 정렬을 위한 추가적인 공간이 필요없는 in-place sorting이다!
  • Unstable Sort이다!! 자리를 찾아가는 과정에서 동일한 값에 대한 순서가 지켜지지 않을 수 있어



삽입 정렬(Insertion Sort)


원리

: 삽입정렬은 현재 보고 있는 위치가 있다면, 그 위치의 전에 위치한 애들을 쭈욱 보면서 현재 위치의 값이 어디에 들어가는 것이 맞는지를 찾아 넣는 알고리즘이다.

조금 더 쉽게 말하자면 1 2 5 4 인 상태에서 현재 보고 있는 위치가 index로는 3인 4라는 값을 보고 있다고 하자. 그럼 5 → 2 → 1 이렇게 차례대로 보면서 4가 어디에 들어가는지를 찾아낸다는 말이다!!

5를 보았을 때는 4보다 크니 pass, 2를 보았을 때는 4보다 작으니 stop!! 결국 2와 5사이가 4가 들어갈 자리라는 것을 알 수 있다


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void insertionSort(vector<int> &arr) {
	for(int i=1 ; i<arr.size() ; i++) {
		int targetIdx;
		int targetNum = arr[i];

		for(targetIdx=i-1 ; targetIdx>=0 ; targetIdx--) {
			if(arr[targetIdx] < arr[i]) {
				break;
			}
		}
		targetIdx +=1;

		for(int j=i ; j>targetIdx ; j--) {
			arr[j] = arr[j-1];
		}
		arr[targetIdx] = targetNum;
	}
}

//처음에는 위처럼 나는 짰지만 더 효율적이게 짤 수 있다
//아래처럼 말이야
void insertionSort(vector<int> &arr) {

	for(int i=1 ; i<arr.size() ; i++) {
		int targetNum = arr[i];
		int j;

		for(j=i-1 ; j>=0 && arr[j]>targetNum ; j--) {
			arr[j+1] = arr[j];
		}

		arr[j+1] = targetNum;
	}
}

특성

  • 위 보이는 것 처럼 O(N^2)이다! 시간복잡도는 worst case를 계산하기 때문이지!! 그러나 정렬이 거의 되어있다고 생각해봐!! 최선의 경우 O(N)만에 가능하게 되어져!
  • 추가적인 공간이 필요없으므로 in-place sort 야!!
  • 동일한 크기의 값에 대해 들어온 순서를 지킬 수 있게 구현할 수 있으므로 stable sort야!



버블 정렬(Bubble Sort)


원리

: 매번 연속된 두개 인덱스를 비교해서, 정한 기준에 의해 두 인덱스의 값을 바꿀지 말지를 비교하는거야.

예를들어, 오름차순이라면 첫번째 인덱스부터 차례대로 인접한 두 인덱스를 비교하여 큰 값이 상대적으로 왼쪽에 있는 경우 두 인덱스의 값을 바꾸어 준다!

이렇게 되면 한바퀴를 다 돌고 난 이후면 맨 오른쪽 위치에는 해당 수들 중 가장 큰 수가 있게 될 것이고 이러한 작업을 반복하면 결국 정렬이 완성되는 것이다.

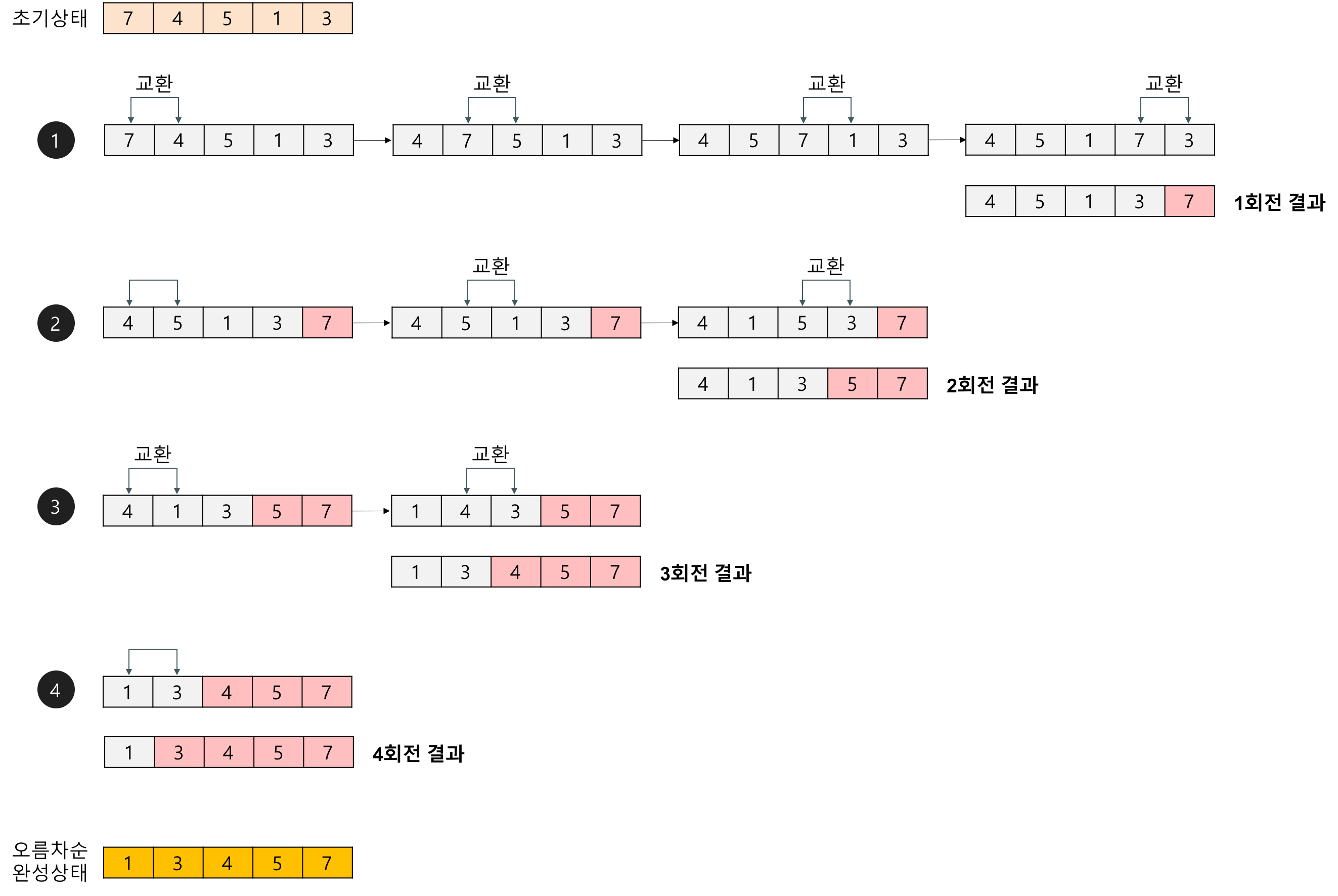
https://gmlwjd9405.github.io/images/algorithm-bubble-sort/bubble-sort.png


코드

1
2
3
4
5
6
7
8
void bubbleSort(vector<int> &arr) {
	for(int i=arr.size()-1 ; i>0 ; i--) {
		for(int j=0 ; j<i ; j++) {
			if(arr[j] > arr[j+1])
				swap(arr[j], arr[j+1]);
		}
	}
}

특성

  • 추가적인 공간이 필요없는 in-place sorting!
  • O(N^2)의 시간복잡도!
  • stable sort야!!



합병 정렬(Merge Sort)


원리

: 배열이 주어졌을 때 해당 배열을 크기가 1이 될 때 까지 계속해서 반으로 분할(divide) 해 나가!!

그리고 더이상 나누지 못하는 상태가 왔을 때 다시 합쳐나가는거지!! 이때 합쳐나갈 때는 정렬을 시키면서 합쳐나가는거야!!

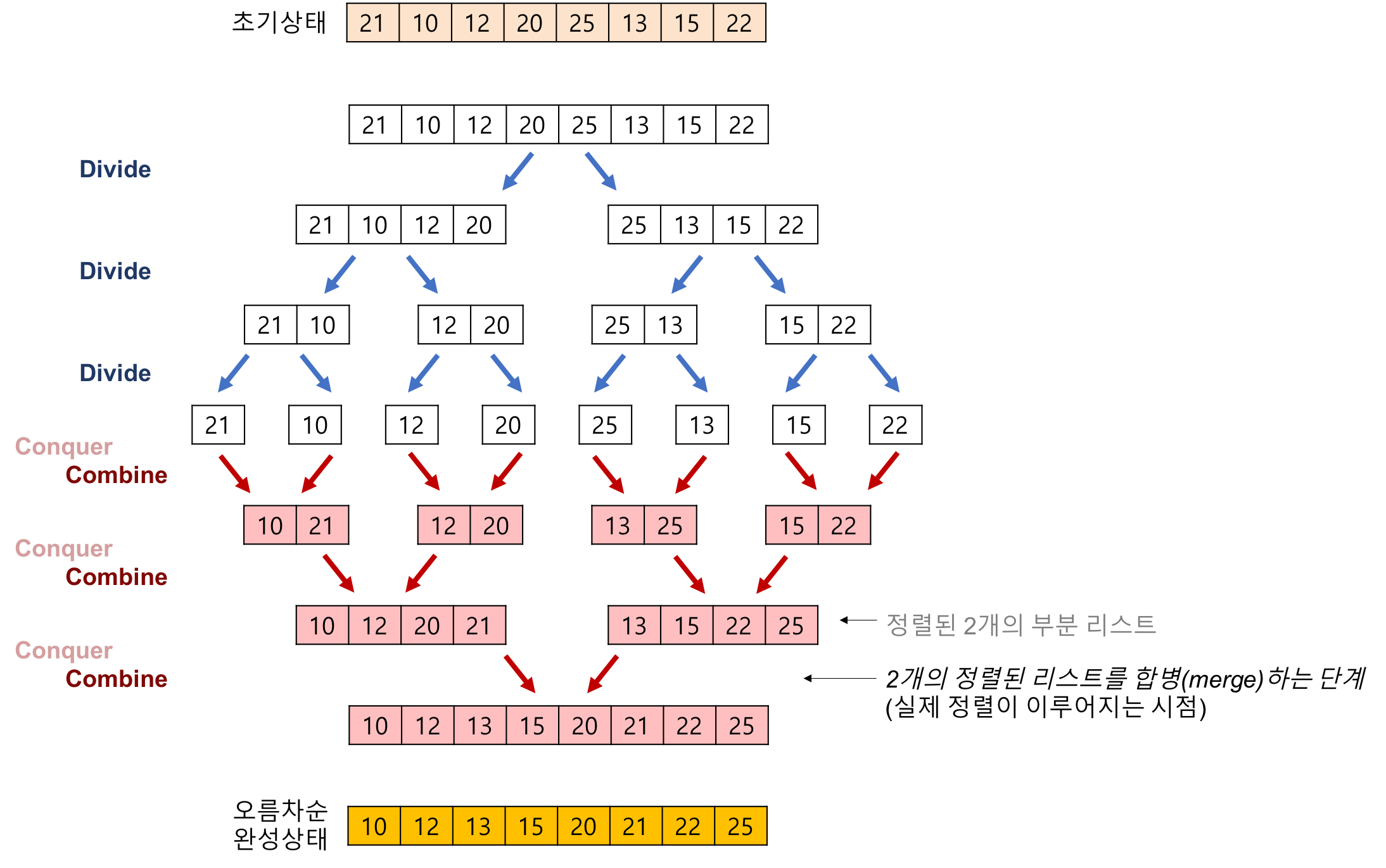
https://gmlwjd9405.github.io/images/algorithm-merge-sort/merge-sort-concepts.png

이렇게 말이야


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void mergeSort(int lt, int rt, vector<int> &arr) {
	vector<int> temp(arr.size());

	if(lt < rt) {
		int mid = (lt+rt)/2;

		mergeSort(lt, mid, arr);
		mergeSort(mid+1, rt, arr);

		int p1 = lt, p2 = mid+1;
		int tempPtr = lt;

		while(p1 <= mid && p2 <= rt) {
			if(arr[p1] < arr[p2])
				temp[tempPtr++] = arr[p1++];
			else
				temp[tempPtr++] = arr[p2++];
		}

		while(p1 <= mid)
			temp[tempPtr++] = arr[p1++];

		while(p2 <= rt)
			temp[tempPtr++] = arr[p2++];

		for(int i=lt ; i<=rt ; i++)
			arr[i] = temp[i];

	}

}

특성

  • 시간복잡도는 O(NlogN) 이다
  • Stable Sort야!!
  • 데이터가 배열 자료구조에 들어가져 있다면 임시 배열이 필요해!! 즉, out-of-place sort야!!
  • 그러나 데이터가 연결리스트로 구현되어 있을 경우 in-place sort 야!! 왜냐하면 연결 링크만 바꾸면서 병합하면 되기 때문이지
  • 분할정복의 한 종류야



퀵 정렬(Quick Sort)


원리

: 퀵 정렬 또한 분할 정복의 한 종류인데 pivot 이라는 기준이 되는 값을 설정 후 이 값을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 나누는 작업을 반복하며 정렬하는 sorting 알고리즘이야!


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int partition(int lt, int rt, vector<int> &arr) {
	int pivot = arr[lt];

	int i = lt;
	int j = rt;

	while(i < j) {
		while(pivot < arr[j])
			j--;

		while(i < j && pivot >= arr[i])
			i++;

		swap(arr[i], arr[j]);
	}

	arr[lt] = arr[i];
	arr[i] = pivot;

	return i;
}

void quickSort(int lt, int rt, vector<int> &arr) {
	if(lt >= rt)
		return;

	int pi = partition(lt, rt, arr);

	quickSort(lt, pi-1, arr);
	quickSort(pi+1, rt, arr);

}

특성

  • 시간복잡도는 평균 O(NlogN)이나 최악의 경우 O(N^2)이 될 수 있어! 언제 최악이 되냐?? 배열이 정렬이 되어있을 수록 효율성은 떨어지지!!
  • 퀵정렬은 최악이 O(N^2)인데도 빠른 정렬로 분류되는 이유가 무엇인가?? 사실 오히려 O(NlogN)보다 더 빠른 성능을 보일 때도 많아
  • 이는 pivot을 어떻게 설정하느냐에 따라 좌우되어지는 것이고 보통 랜덤으로 하는 방법을 선택하나 left, right를 통해 mid 값을 뽑아내서 최악의 case를 피할수도 있어!
  • Unstable Sort야!!



힙 정렬(Heap Sort)


원리

: 완전 이진트리를 기본으로 하는 힙 자료구조를 기반으로 한 정렬이야

오름차순 정렬을 원할 때는 최소 힙을 사용하고 내림차순 정렬을 원할 때는 최대 힙을 사용해!

힙에 대해서는 따로 정리를 하는 것으로 하자!


특성

  • O(NlogN)이라는 시간 복잡도를 가지고 있어! 완전이진트리인 힙 자료구조를 이용하기에 요소를 힙에 삽입하거나 혹은 삭제하여 재정비할 때 logN만큼의 시간이 들지! 그리고 요소의 갯수가 N이니 O(NlogN)이 나오는거야
  • 당연히 Unstable Sort야!!
  • 정렬을 위한 extra memory는 필요 없기에 in-place sort야!



쉘 정렬(Shell Sort)


원리

: 쉘정렬은 삽입정렬을 보완한 알고리즘이야. 삽입정렬이 언제 효율지 좋다 했는지 기억이 나는가!? 위에 적혀있겠지만 거의 정렬이 된 상태에서 효율이 최대로 나오지.

이런 아이디어에서 나온 것이 쉘 정렬이야. 전체적으로 어느정도 정렬된 상태로 만든 후 삽입정렬을 하는 거지!!

구체적으로는 간격(gap)을 구해서 그 간격만큼의 위치에 있는 원소들을 추출해서 각각의 부분리스트를 만들고 그 각각에 대해 정렬을 한 후 새로이 gap을 설정하고 반복하는 거지!!

그러다 gap이 1이 되었을 때는 삽입정렬 한번 시행하면 모든 요소들이 정렬된 상태로 나오게 되는 것이지!

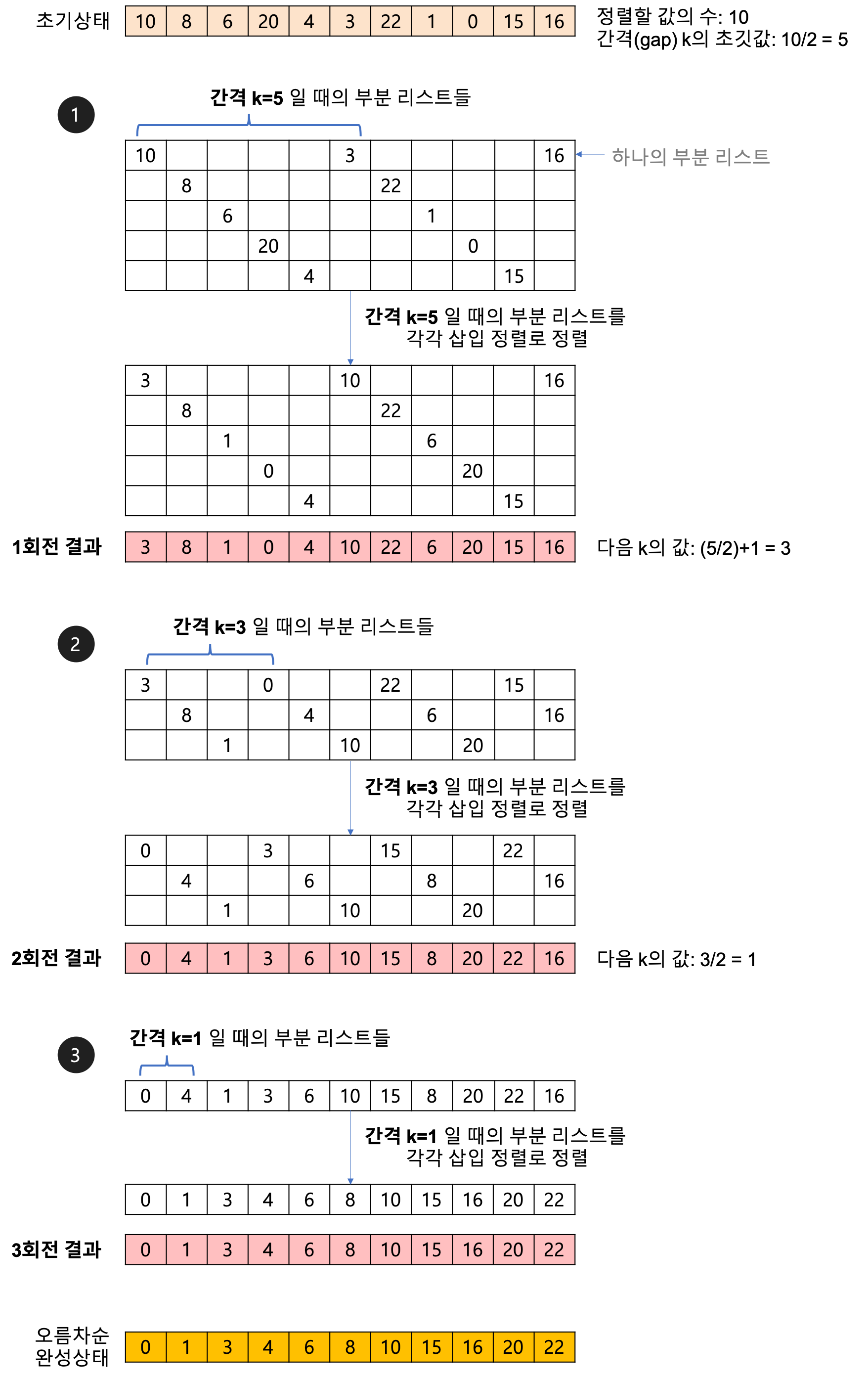
이런식으로 되어지는거야!

간격의 초기값은 (정렬할 값의 수)/2로 구할 수 있어. 그 이후 각각의 간격에 대해 /2 연산을 진행하면서 구해나가면 돼! 이때, 간격은 홀수로 하는 것이 좋기에 간격/2 연산의 결과가 짝수라면 +1을 해줘!


특성

  • 평균적으로 O(N^1.5)의 시간복잡도를 가져!! Wort일 때는 삽입정렬과 동일하게 O(N^2) 이야







https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html

sortingalgorithm