선형자료구조

: 선형자료구조란 하나의 자료뒤에 하나의 자료가 존재하고 이것들이 순차적으로 나열되어있는거지. 즉 자료들 간의 앞뒤 관계가 1:1의 관계라는거야

배열

: 여러 데이터를 하나의 이름으로 그룹핑해서 관리하기 위한 자료구조야!! 배열은 정의와 동시에 길이를 지정하며 바꿀수가 없어.

하지만 인덱스를 활용하여 빠르게 조회가 가능하다는 장점이 있어.

물론 삭제의 경우도 인덱스를 접근하여 빠르게 지우는 것이 가능하나 여기서 지운다는 의미는 null, 혹은 0과 같은 ‘없음’을 의미하는 값을 넣는 것이고 결국은 메모리 공간을 차지하게 되는 단점이 있다.

리스트

: 리스트와 배열의 차이를 굳이 따지자면 고정된 크기라고 생각해. 배열은 할당받은 크기가 고정되어있지만 리스트는 필요에 따라 조정할 수 있는거지. 리스트에는 두가지 종류가 있어. 순차 리스트와 연결 리스트야.

순차 리스트

: 순차리스트는 배열을 이용하여 구현되어 있어. 우선 순차 자료구조는 구현할 자료들을 논리적인 순서대로 메모리에 연속하여 저장하는 구조야!! 즉 따닥따닥 빈자리 없이 순서대로 저장된다는 거지!

순차리스트는 데이터를 삽입하거나 삭제하고나면, 연속적인 위치를 유지하기 위해 원소를 옮기는 추가작업이 필요해 → 비효율적이지

그러나 내부적으로 배열로 구현이 되어있기에 인덱스를 통해 접근이 빠르다는 장점이 있어!

연결 리스트

: 그럼 연결리스트는 무엇이냐. 우선 연결 자료구조는 메모리에 저장된 데이터의 위치,순서가 상관이 없어. 논리 메모리에 따닥따닥 붙어진 상태로 할당받지 않아도 된다는 거야! 왜냐? 연결자료구조는 노드라는 각각의 독립된 공간에 데이터를 담은 후 링크를 통해 논리적인 순서를 표현하기 때문이야.

이렇게 구현하면 어떤 장점과 단점이 있는가하면,

삽입과 삭제시 노드의 링크만 수정하면 되기에 순차리스트에 비해 연산속도가 빨라

그러나 탐색하는 부분에서는 순차리스트가 더 효율적이지. 왜냐?! 순차 리스트는 배열로 구현되어 있어서 인덱스를 통해 원소를 바로 탐색할 수 있으나 연결 리스트의 경우 처음부터 다음 노드들을 탐색해야 하기 때문이야!! 특정 노드의 접근할 수 있는 노드는 정해져있거든(그 전 노드 or 그다음 노드, 이건 양방향 연결 리스트의 여부에 따라 나뉜다).

결론적으로 추가 및 삭제에서는 연결리스트가, 탐색에서는 순차리스트가 더 효율적인 자료구조라고 볼 수 있어

스택 (Stack)

: 스택은 LIFO(Last In First out) 형태의 자료구조야! 즉 먼저 들어간 녀석이 나중에 나온다는 거지!

크게 push 와 pop 연산으로 나뉘고 각각 데이터를 넣는 것과 빼는 것에 해당해.

이때, stack 크기 이상의 자료를 넣으려고 할 경우 stack overflow가 발생할 수 있으며 stack이 비어있는데 pop을 하려할 경우 stack underflow가 발생할 수 있다!!

배열과 연결리스트로 구현할 수 있는데 일반적으로 배열을 사용하는 것 같다.

배열을 이용할 경우 size가 fix 되지만 연결리스트 경우 그렇지는 않다! 그렇나 공간을 동적으로 받고 지우는 과정에서 소요시간이 더 걸리게 되는 것이다.

지역변수 저장, 임시데이터 백업, 함수 호출 순서 제어, 인터럽트, try catch stack unwinding 등에 쓰여

큐 (Queue)

: 큐는 FIFO(First In Frist Out) 형태의 자료구조야! 즉 먼저 들어간 녀석이 먼저 나온다는 거지! 스택과는 상반된 녀석이라고 생가하면 될 것 같네.

큐의 종류

1. 선형 큐 (Linear Queue) : 기본적인 큐의 형태로 긴 막대모양의 큐라 생각하면 돼! 제한된 크기에서 dequeue과정을 통해 생긴 앞 부분의 공간을 채우기 위해 자료를 한칸 씩 옮기거나 그렇지 않으면 공간을 낭비하게 되는 문제가 생겨
2. 원형 큐 (Circular Queue) : 위와 같은 선형큐의 문제점을 해결한 형태라고 볼 수 있다. 배열의 마지막 인덱스에서 다음 인덱스로 넘어갈 때 (index+1)%(배열 사이즈) 를 통해 마치 원형으로 구조되어있는 것 처럼 앞의 빈 부분을 활용할 수 있는 구조로 큐를 짠 것이다!
3. 우선순위 큐(Priority Queue) : 우선순위큐는 데이터가 들어간 순서가 아닌 설정되어있는 우선순위에 따라 우선순위가 높은 데이터부터 꺼내도록 구현된 큐이다! 일반적으로 힙을 이용하여 구현해!

덱 (Deque)

: 양쪽 끝에서 삽입과 삭제가 모두 가능한 자료구조야!!

비선형자료구조

그래프

: 그래프는 정점과 간선으로 이루어진 자료구조야! 정점 즉 vertex 간의 관계를 간선(Edge)를 이용해 표현한 자료구조라고 볼 수 있지.

그래프를 구현하는 방법에는 크게 인접행렬(Adjacency Matrix)와 인접리스트(Adjacency List)가 있어.

인접행렬로 구현한 그래프

• 이렇게 인접행렬로 하면 두 Vertex간의(a,b) 관계를 O(1)에 알 수 있어 (graph[a][b] 이렇게!!)
• 구현이 인접리스트에 비해 간편해
• 그러나 전체 연결 상태를 파악하기 위해 2차원 인접행렬을 뒤져야하는데 그럼 O(N^2)이라는 비효율적인 시간을 들이게 돼!!
• 그리고 연결 정보가 없는 부분에 대해서도 공간을 할당하고 있기에 낭비되는 공간도 있지

인접리스트로 구현한 그래프

• 정점들의 연결정보를 볼 때 간선의 갯수 만큼 보면 돼!! (양방향이면 2배겠넹!! 그래도 인접행렬보다 효율적이지)
• 필요한 공간만 사용하기에 낭비가 적어
• 그러나 구현이 인접행렬에 비해서는 조금 어려우며 특정 두 vertex의 연결상태를 확인하는 데에는 인접행렬보다는 조금 더 시간이 걸리지

트리

: 트리는 그래프의 종류라고 볼 수 있으나 차이점이 있어!! 그래프에는 없는 트리에는 루트가 존재하고 그 루트를 기준으로 계층을 이루고 있어!! 그리고 사이클은 존재하지 않아!

이진트리

1. 이진 트리 : 모든 내부 node들이 둘 이하의 자식 node를 가지는 트리
2. 완전 이진 트리 : 가장 마지막 레벨을 제외한 모든 노드들이 두개의 자식을 가지는 것으로 꽉 차 있고 마지막 레벨은 왼쪽부터 마지막 노드까지 빈칸이 없이 차있는 트리
3. 포화 이진 트리 : 마지막 level까지 완전히 꽉 차 있는 이진트리

BST (Binary Search Tree)

: 이진탐색트리란 이진트리의 한 종류로써 키 값을 보다 빠르게 찾을 수 있게 구조한 트리이다. 중복은 허용되지 않으며 하위트리들 또한 이진탐색트리가 된다!

다음과 같은 규칙이 있다.

• 노드의 왼쪽 하위 트리에는 노드의 키보다 작은 키가있는 노드만 포함
• 노드의 오른쪽 하위 트리에는 노드의 키보다 큰 키가 있는 노드만 포함

이진탐색트리는 한쪽으로 편향된 형태를 가질 수가 있어!! 그럼 이러한 한쪽으로 편향된 트리를 균형잡히게 만들 수 있는 방법은 없을까?? 다음을 보자

균형잡힌 트리

B-Tree

: B트리는 균형잡힌 트리이기는 하지만, 이진트리는 아니야.

B트리는 하나의 노드에 여러개의 데이터를 가질 수 있어!! 그리고 그 데이터의 갯수 + 1 만큼 자식을 가질 수 있는거지.

이렇게 생겨먹은 놈이야!!

각 노드는 정렬된 상태여야해!

위의 그림에서도 알 수 있듯이, BST와 비슷하게 특정 KEY의 왼쪽은 해당 KEY보다 작은 값으로 구성된 노드들이 있고 오른쪽에는 해당 KEY보다 큰 값으로 구성된 노드들이 존재해!

다음과 같은 규칙이 있어

• Root 노드가 Left node인 경우를 제외하고는 항상 2개이상의 자식을 가져야해
• 차수를 M이라고 했을 때 루트 노드를 제외한 모든 노드는 M/2개의 키를 가지고 있어야해!
• 모든 Leaf Node 들은 같은 level에 있어야해!
• 노드의 key 값들은 오름차순이며 중복을 허용하지 않아!
• 차수가 홀수냐 짝수냐에 따라 알고리즘이 조금 틀려
• 특정 key의 왼쪽 서브트리는 그 key보다 작은 값, 오른쪽 서브트리는 그 key 보다 큰 값들이야.

1) 삽입

: 삽입할 때에는 BST처럼 삽입하고자 하는 데이터의 크기를 노드에 존재하는 key 값들과 비교해 작으면 왼쪽자식으로, 크면 오른쪽 자식으로 타고 내려가면 돼!! 만약 다 타고 내려왔을 때 해당 노드에 데이터를 담을 수 있는 공간이 있다면 넣으면 되고, 없다면 분할하는 작업을 수행해야해!!

분할작업은 간단해. 넘친 데이터들 사이에서 중간 크기의 값을 해당 노드의 부모노드로 올려주는거야!!

올려주었을 때 올림을 받은 노드 입장에서도 노드가 수용할 수 있는 데이터 갯수를 넘었다면 또 반복해서 분할 작업을 수행하면서 부모노드로 올려주면 되는거야!

2) 삭제

: 삭제는 그때그때, case 별로 경우가 많아 아래 참조에 있는 링크를 확인한 후 이후 공부해서 추가하자.

B+-Tree

: B Tree와 굉장히 비슷하게 생긴녀석이야!! 그렇다면 뭐가 다르냐?? 리프노드가 연결리스트 형태로 되어있어서 리프노드들간의 선형검색이 가능하게 되어있어!!

데이터베이스의 Index를 구성하는 대표적인 자료구조이기도 해!

요런 인덱스 형태 즉 멀티레벨 인덱싱인데 이 형태를 B+ TREE로 나타낼 경우 아래와 같이 되는거지.

구체적으로 B Tree와의 차이점은 다음과 같애

• 모든 key, data가 리프노드에 모여있어!! B tree 같은 경우네는 리프노드가 아닌 노드들도 각자 key마다 데이터를 가지는 반면, B+ tree는 리프노드에 모든 data를 가지는 형태야
• 모든 리프노드가 연결리스트 형태를 뛰고있어! 그렇기에 검색을 할때 좋은 시간복잡도로 효율적으로 탐색이 가능하지
• 리프토드의 부모 key는 리프노드의 첫번째 key보다 작거나 같애

AVL Tree

: AVL트리와 이진탐색트리는 굉장히 비슷하지만 균형을 맞춰주는지의 여부에서 차이점이 존재해!

AVL 트리는 균형잡힌 트리로써 균형인수(Balance Factor)를 사용하여 균형을 맞춰줘!!

그럼 이 Balance Factor가 무엇이냐?? 왼쪽과 오른쪽 서브트리의 높이 차야!!

그리고 이 Balance Factor가 -1, 0, 1일 때만 균형있는 트리라고 보고 그 외의 값이 계산될 경우 트리를 조정해줌으로써 균형을 맞춰주는거지!

균형을 맞지 않은 경우는 크게 4가지 형태를 띄어

1. LL
2. LR
3. RL
4. RR

이렇게 말이야!! 저건 어디로 쏠려있는지의 모양을 나타내는 것이고 균형도 즉 Balance Factor가 양수인지 음수인지를 보면 어디로 쏠렸는지 알 수 있어.

양수라면 왼쪽으로, 음수라면 오른쪽으로 쏠려있는 트리라는 것이겠지.

결국은 이 쏠림 현상을 균형있는 ㅅ 모양으로 맞춘다고 생각하면 쉽게 이해할 수 있을거야.

Red-Black Tree

: 레드블랙트리도 이진트리의 종류이나 균형이 맞혀져있는 트리야! 즉 Balanced Binary Search Tree라고 말할 수 있지. 그럼 Red Black Tree 요 녀석은 어떻게 균형을 맞추는가? 이름에서 알 수 있듯이, 검정색과 빨강색을 이용하여 맞춰져!! 조금 더 자세히 보자.

균형을 맞추기 위한 조건은 다음과 같애

1. 루트노드의 색깔은 검정이야
2. 모든 리프노드의(External Node)들은 검정이야
3. 빨강 노드의 자식은 검정이야. (즉 빨강색 노드의 자식이 빨강색일순 없는거지)
4. 모든 리프노드에서 Black Depth는 같애 (즉, 리프노드에서 루트노드까지 가는 경로에서 만나는 블랙노드의 개수는 같애)

위 4개의 조건이 레드블랙트리를 균형잡힌 트리로 만들 수 있게 해주는거야.

삽입

: 삽입 할 때에는 삽입하는 노드는 우선 무조건 빨강이야. 그리고 해당 노드를 이진트리 조건에 맞추어 삽입을 하면 위 4가지 조건에 어긋나는 경우가 발생할 수 있어.

여기서 3을 넣으면

이렇게 되는 것 처럼!!

이러한 상황을 Double Red라고 해!!

그럼 이때 어떻게 하는가?? 두가지 해결방법이 있어.

1. Restructuring
2. Recoloring

그럼 위 두개는 어떤 상황에 각각 쓰는가?? 그것은 insert된 노드의 uncle node의 색깔에 따라 결정이 되어지는거야!!

이렇게 uncle 노드의 색깔이 검정일 때는 Restrucutring

uncle 노드의 색깔이 빨강일 때는 Recoloring을 수행해

먼저 Restructuring을 보자

Restructuring은 다음과 같은 단계를 거쳐서 이루어져

1. insert한 노드와, 그 노드의 부모, 그 노드의 조부모를 오름차순으로 정렬해
2. 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만들어
3. 부모로 만들어진 녀석을 검정으로 만들고 나머지 두 자식을 빨강으로 만들어
4. 기존에 있던 자식을 붙여

이 녀석을 정렬하여 중앙 값을 부모로 만들면

이렇게 되겠지!! 그리고 색깔을 올라간 부모를 검정, 자식들을 빨강으로 바꿔죠

이렇게 말이야!!

그 이후에 기존에 있던 자식을 붙여주면 돼!!

다음으로 Recoloring을 보자

Restructuring은 다른 서브트리에 영향을 주진 않지만 Recoloring 은 달라!! 그래서 한번의 동작으로 끝나지 않을수도 있어!!

먼저 그 과정을 보면 다음과 같애

1. 현재 insert된 노드의 부모와 그 형제를(unclde) 검정으로 한 후 조부모를 빨강으로 해!
2. 조부모가 Root Node가 아닐시에 다시 Double Red가 발생할 수 있어!! (만약 Root Node라면 규칙에 의해 Root Node는 검정색으로 다시 바뀌어)

현재 이러한 상태에서 삽입된 녀석 6을 기준으로 부모와 부모의 형제를 검정으로 바꾸어주면

요렇게 되는거야!!

그리고 조부모를 빨강으로 만들어줘!!

이러한 상태에서 만약 4가 Root Node라면 다시 검정으로 셋팅이 되겠지!!

하지만 만약 아니라면…??

4위에 다른 부모노드가 존재한다면..?? 그리고 그 노드가 빨강색이라면…?

그럼 다시 Double Red가 발생하겠지..?

그럼 또 uncle node의 색을 보고 Restructuring 과 Recoloring 중 하나의 연산을 수행해야겠지..

힙 (Heap)

: 힙은 완전이진트리의 한 종류로 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조야!

힙은 일종의 반정렬 상태를 유지해!! (완전한 정렬은 아니고 최대힙이라면 큰 값이 상위 레벨, 작은 값이 하위 레벨에 있는 요정도의 정렬상태)

힙은 중복된 값을 허용해 (bst는 허용하지 않지)

힙은 두 종류가 있어.

1. 최대힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전이진트리
2. 최소힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전이진트리

힙을 쉽게 구현하는 방법으로는 배열을 이용할 수 있어. 배열을 이용해서 이진트리를 나타내는 방법은 알지?

• 왼쪽 자식 인덱스 = 부모 인덱스 * 2
• 오른쪽 자식 인덱스 = 부모 인덱스 * 2 + 1
• 부모 인덱스 = 자식 인덱스 / 2

이렇게야!

힙의 삽입

: 먼저 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입해!

그리고 그 노드에서부터 부모 노드와 비교하면서 올라가면서 자신의 자리를 찾아나가!!

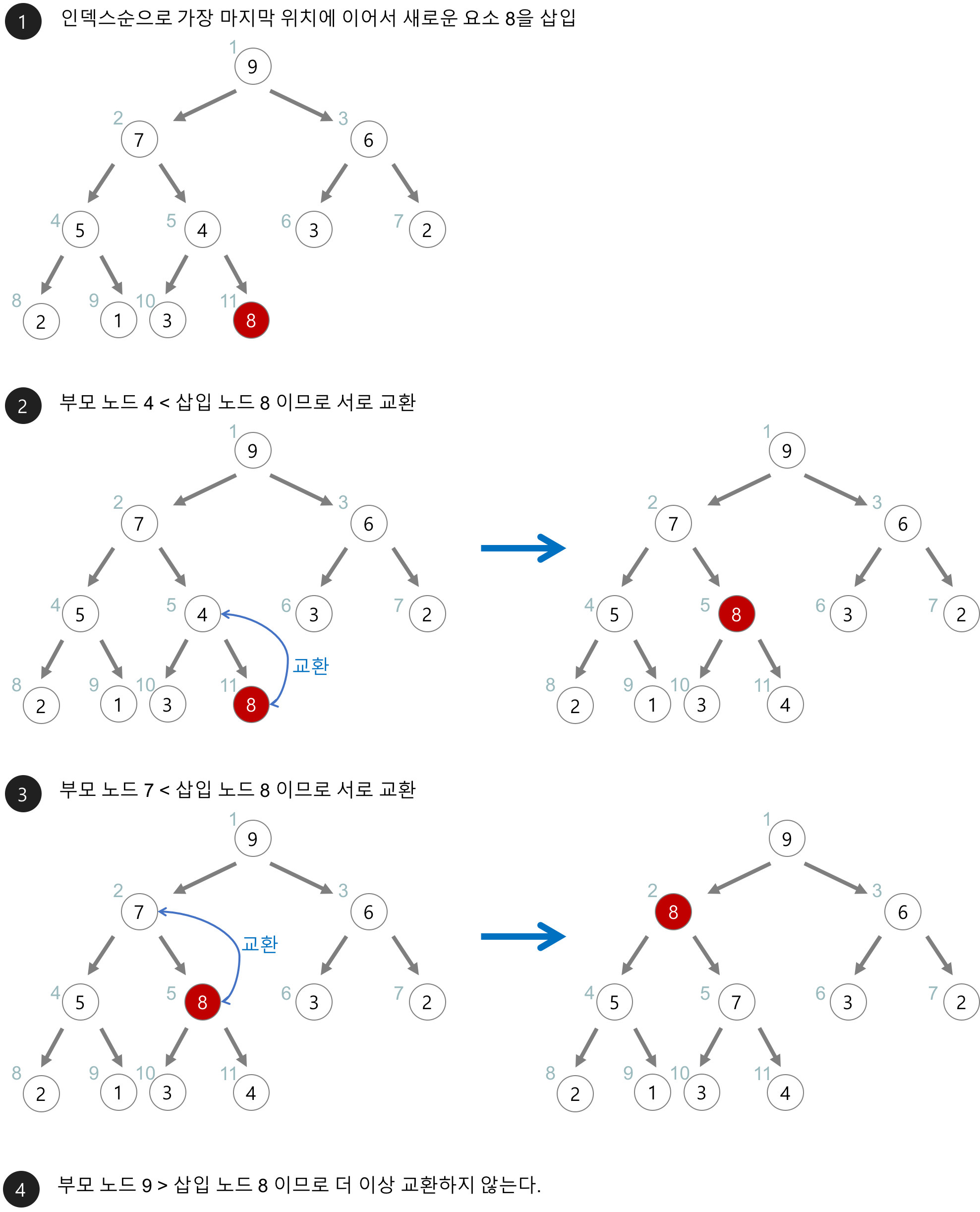
이런식으로 말야!!

힙의 삭제

: 힙에서 데이터를 꺼내는 것은 결국 최댓값 혹은 최솟값을 사용하기 위해 빼낸다는 거겠지.

힙의 구조상 루트노드가 삭제되는 상황이야.

루트노드를 삭제한 후 루트 노드 자리에는 힙의 마지막 노드를 가져와서 넣어!

그리고 힙을 재구성하는데 이때 루트부터 시작해서 자식 노드들과(왼쪽, 오른쪽 자식) 비교해서 큰 자식 노드와 교환하면서 내려가!

이러한 과정을 현재 보고 있는 대상이 되는 노드가 자식 노드들 보다 클 경우 멈춰 ( 최대 힙의 경우겠지, 최소힙이라면 작을 경우 멈추면 돼)

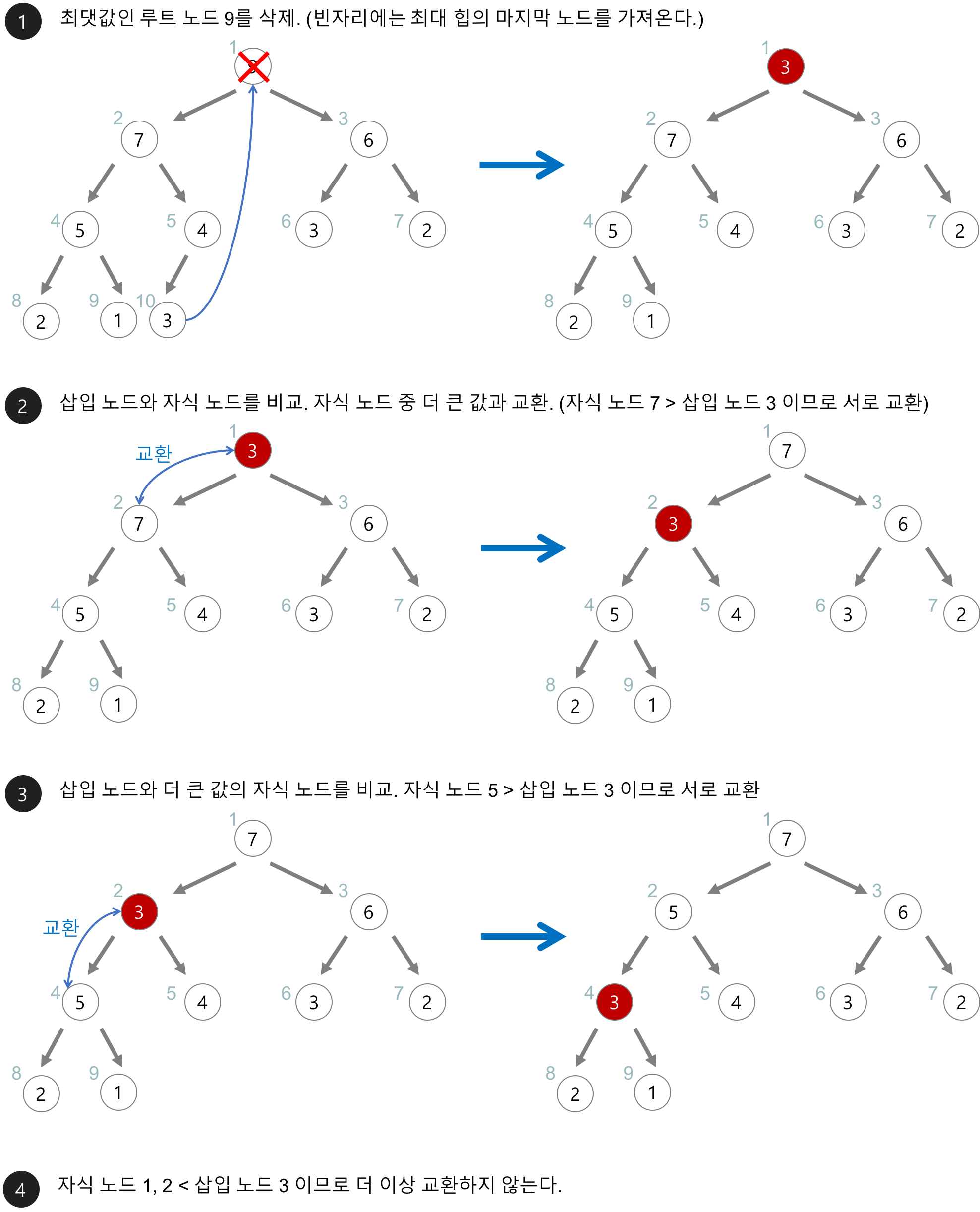
이렇게 말이야!!

해쉬 (Hash)

원리

: 키값을 해시 함수라는 수식에 대입시킨 후 나온 결과를 주소로 사용하여 값에 접근하는 자료구조를 뜻해

해시함수는 키 값을 값이 저장된 주소 값으로 바꾸기 위한 수식이라고 생각하면 될 것 같애.

해시테이블은 무엇이냐. 위에서 해시함수를 통해 키를 해시값으로 매핑한다고 했는데 이 해쉬값을 색인(index) 혹은 주소 삼아 데이터의 값을 키와 함께 저장하는 자료구조를 해시테이블이라고 해!

하지만 다른 키 값에 대해 같은 인덱스가 나오는 경우도 발생할 수 있겠지?? 이를 충돌이라고해.

이를 해결하는 방법에 대해 보자

충돌 해결

1) Open Addressing

: 충돌 바생시 다른자리에 대신 저장하는 것을 이야기해.

다른 자리를 정하는 방법에도 여러가지가 있어.

먼저 선형조사법은 충돌 발생시 바로 다음 자리를 확인하여 비어있으면 넣어줘. 보다시피 간단해! 하지만 이렇게 넣을 경우 특정 영역에 값이 몰리는 현상이 발생할 수 있겠지

이차 조사법은 n제곱 칸 옆을 확인하는거야! n은 하나씩 증가하는 자연수라고 보면 될 거 같애! 이러한 방법은 선형조사법에 비해서는 몰리는 현상을 완화시킬 순 있겠지. 하지만 한곳에서 계속해서 충돌이 발생한다면 여전히 클러스터 현상이 보일 수 있어.

이중해쉬는 선형조사법과 이차 조사법의 단점을 해결하고자 한 방법이야. 이름처럼 해쉬함수를 2개 사용하는 것이지. 두번 째 해시함수를 둠으로써 충돌했을 때 몇 칸 다음을 볼지를 정하는 방법을 도입한거야. 이렇게 할 경우 클러스터 현상을 막을 수 있어

2) Chaining

: 이는 다른 자리에 대신 저장하는 것이 아닌 연결리스트를 이용하여 그 자리에 계속해서 연결해 나가는 방식이야.

연결리스트라고 하였지만 연결리스트 대신에 트리를 활용할 수도 있어. 그럼 탐색속도면에서 효율적인 부분을 가질 수 있겠지.

https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

https://zeddios.tistory.com/237

https://coding-factory.tistory.com/610

https://velog.io/@emplam27/자료구조-그림으로-알아보는-B-Tree